Scaling Laws for Optimal LR and Batch Size - Part IIb

Troubleshooting the fit

Introduction

Welcome back. In Part I and Part II of this series, I fit scaling laws for optimal batch size B^* and optimal learning rate \eta^*, most recently obtaining the fit

\(B^{*} = 115.8 N^{-0.027} D^{0.365}\)

\(\eta^{*} = 0.332 N^{-0.493} D^{0.191}\)

In contrast, Li et al. 2025 obtained larger-magnitude exponents on dataset size D for both scaling laws, as well as on model size N for the learning rate scaling law. What explains the difference?

More Data

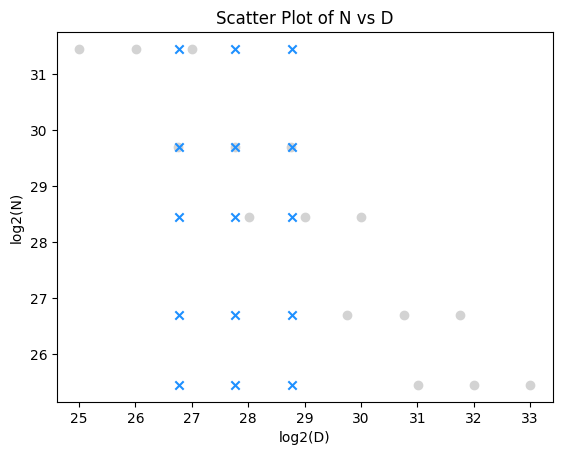
The simplest explanation is insufficient data collection of some kind. For example, despite adding grid data (blue) as well as iso-FLOP curve data (gray), the coverage is still lacking in the upper-right, corresponding to a more compute-expensive regime.

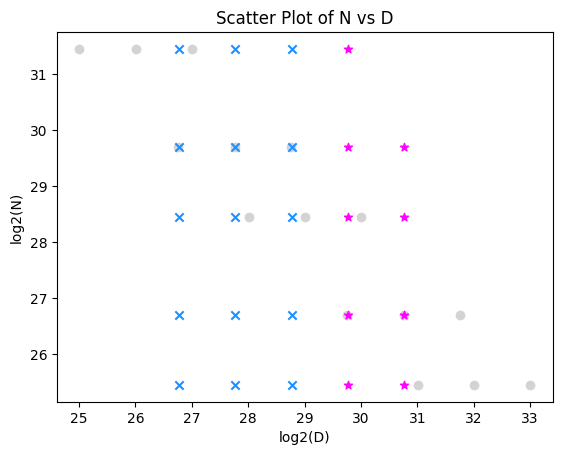
Let’s see if an increase in compute budget can resolve the discrepancy. I will extend the (N, D) grid of runs in the last post, using 2x-4x larger dataset budgets D than the previous largest, and expanding the coverage of the grid rightward (below, magenta).

Combining all data, I got the following fitted scaling laws:

\(B^{*} = 353.3 N^{-0.061} D^{0.342}\)

\(\eta^{*} = 0.917 N^{-0.525} D^{0.171}\)

This is not better. Compared to the fit we already had from the blue and gray points, adding the magenta ones did not move the exponents much.

Bootstrapping

I also tried bootstrapping and parameter averaging to improve the robustness of the regression coefficients, following Li et al., 2025. The sampling can be implemented straightforwardly in Pandas by using the DataFrame ‘sample’ method with replace=True, and the parameter averaging can be implemented straightforwardly using the StatsModels library by averaging the regression coefficient DataFrames.

I averaged over 10k bootstrapped samples of the OLS regression coefficients from log-log space, and converted the result to the scaling law format after, obtaining:

\(B^{*} = 367.4 N^{-0.063} D^{0.341}\)

\(\eta^{*} = 0.969 N^{-0.526} D^{0.170}\)

This is not better either. It is close to the values in the vanilla OLS estimate.

Exploratory Data Analysis

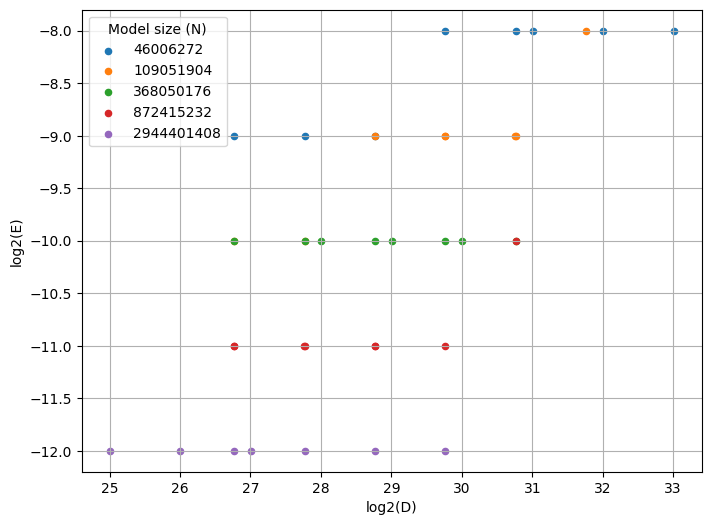
As a last-ditch hope to improve the results, I visualize the scatterplots of optimal learning rate w.r.t. dataset size D, similar to Figure 6(a) of Li et al., 2025.

Interestingly, the slopes for the different model sizes N look potentially different from each other, which is contrary to our hypothesis that

\(\log \eta^{*} = \log c_{\eta} + \alpha_{\eta} \log N + \beta_{\eta} \log D\)

for some c_{\eta}, \alpha_{\eta}, \beta_{\eta} independent of N. To investigate this issue and disambiguate it from quantization in the learning rate sweep, next time we’ll double the learning rate granularity, redraw this figure, and refit the scaling laws.

Conclusion

In this post, I found larger token budgets D did not significantly improve the fit of the hyperparameter scaling laws. I also tried bootstrapping and parameter averaging, but found this did not resolve the issue either. Finally, I identified that the learning rate granularity was possibly insufficient, prompting me to begin a refreshed set of experiments with double the sweep granularity, with results reported next time.