Scaling Laws for Optimal LR and Batch Size - Part XI

Is the loss surface w.r.t. LR truly convex?

Aug 06, 2025

Introduction

In the StepFun paper, the authors claim that the cross-entropy loss of language models is a convex function of batch size and learning rate.

Following my attempts to fit hyperparameter scaling laws with the same functional form as theirs, in this post I attempt to validate the extrapolation performance, and also investigate the described convexity property.

Background

In the previous post, I fit scaling laws for optimal batch size and learning rate as a function of model size and token budget. Preliminary analysis suggested that an architecture similar to OLMo-1 worked best for extrapolation quality, but I did not rigorously validate this in the previous post.

In this post, I ran the same training setup, but with (N, D) = (4.7 * 10^9, 100 * 10^9), and swept over the learning rate \eta while using a batch size B close to the predicted optimum of ~2M.

Results

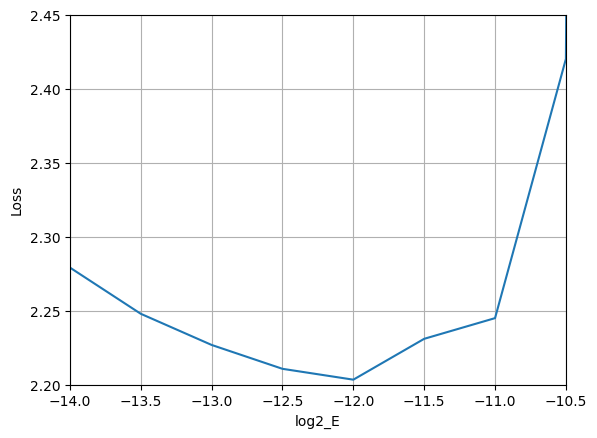
Sweeping over the learning rate \eta from 2^-14 to 2^-9.5 in multiples of 2^0.5, I obtained the following loss surface with respect to LR:

Analysis

It can be seen that the sweep optimum is at 2^-12 = 0.00024414062, which is close to the forecasted optimum of ~0.0003 from the previous post. For reference, log2(0.0003) is approximately -11.7, right between the empirical log-optimum at -12 and the next increment at -11.5.

Interestingly, the empirical loss surface is not quite convex w.r.t. the learning rate. It can be seen that between log2(\eta) = -12 and log2(\eta) = -11, there is a strictly concave region. It practice, this may not matter a lot, because the loss surface still appears monotonically decreasing prior to the global minimum, and monotonically increasing after it. But it is still worth pointing out that the claimed convexity property may not hold perfectly in practice.

Conclusion

In this post, I discussed the extrapolation quality of the hyperparameter scaling laws fit in Part X of this series, and validated that the OLMo-1 architecture yields scaling laws with good extrapolation.

In addition, I observed that the obtained empirical loss surface w.r.t. LR had no local minima besides the global minimum, but also found that the empirical loss surface was not necessarily convex w.r.t. LR.