Introduction
In Part X of this series, I fit scaling laws for optimal batch size and learning rate using the AdamW optimizer applied to a Transformer architecture similar to OLMo-1. In Part XI of this series, I validated the obtained scaling laws’ forecasts on models with 4.7 billion parameters trained on 100 billion tokens.
In this post, I will repeat the scaling law experiments from Part X, but this time using the Muon optimizer.
Muon Setup
Muon applies to 2D linear projections only.
In this post, I apply the Muon optimizer to all 2D parameters inside the residual blocks of the Transformer. In particular, all linear projections for queries, keys, and values are 2D projection matrices, with the heads obtained afterwards by reshaping the output of the projections. Instead of using Muon for the embeddings and unembeddings, I use AdamW for these parameters, following Jordan et al., 2024. Following the design of OLMo-1, there are no trainable bias parameters in the model, and due to nonparametric RMSNorm, there are also no trainable scale parameters.
Following Liu et al., 2025, the learning rate for each 2D projection optimized by the Muon optimizer is given by
while the learning rate for the parameters optimized by AdamW is simply \eta. As suggested by Wortsman et al., 2023, I use independent weight decay, which I apply to all parameters, with \lambda = 1e-5.
Scaling Laws Setup
Open codebase. I use the research codebase at https://github.com/lucaslingle/babel with branch name ‘nonparametric_scaling_muon’.
Architecture. I use an architecture similar to OLMo-1, with nonparametric RMSNorm applied to the residual block inputs. I use SwiGLU nonlinearities in the MLP sublayers, with d_ff = 3 * d_model. I use d_head = 128, and n_head = d_model / d_head. I use a locked aspect ratio of d_model/n_layer = 128.
Optimization. I use Muon with \mu = 0.95 and AdamW with \beta1 = 0.9, \beta2 = 0.95, \eps = 1e^-8. The learning rate schedule uses 2% warmup, followed by cosine decay to a 0.1x factor of the peak.
(N, D) grid. For efficiency, I use model sizes N = 46M, 109M, 368M and dataset sizes D = 128M, 256M, 512M, 1024M.
(B, \eta) grid. I sweep over batch sizes from 32768 to 2097152 in powers of 2, sweep over learning rates from 0.00012207031 to 0.0078125 in powers of 2^0.5.
Training data. I use the 350B token sample of FineWeb, and the LLaMA-2 tokenizer, which has approximately 32000 vocabulary items including special tokens.
Evaluation. I use 100 held-out batches of size 2097152 tokens for loss evaluation. Evaluation occurs after training has concluded.
Scaling Laws Result
I obtained the following fitted scaling law, again omitting Akima spline interpolation and bootstrapping for simplicity.
The Optimal Batch Size
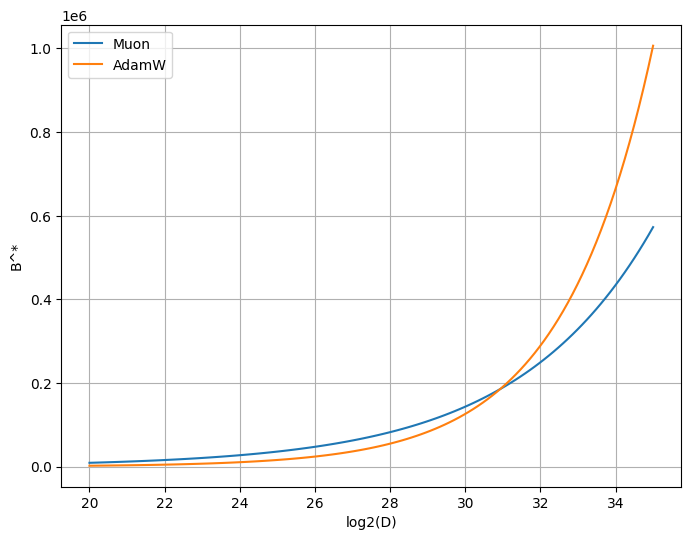
The scaling exponent for optimal batch size is quite interesting: it is far smaller (0.4) compared to AdamW (0.6). The proportionality constant however is far larger (34.95) compared to AdamW (0.480).
The hesitant conclusion here is that the optimal batch size for Muon is larger than that of AdamW for a transient period, but is in fact asymptotically smaller.
The chart below illustrates the optimal batch size scaling law for both optimizers:
These scaling laws suggest that for dataset sizes D above around log2(D) = 31, the AdamW optimal batch size is in fact larger than the Muon one. Interestingly, this occurs at D = 2.1 * 10^9, or 2.1 billion tokens, which is quite small indeed.
This conclusion will need some empirical verification later, but if correct it seems to contradict the prevailing wisdom that Muon likes a larger batch size.
One additional wrinkle here is that we are only measuring the optimal batch size—but Shah et al., 2025 has suggested that for very very large batch sizes, the performance of Transformer models trained by Muon degrades less than when those same very large batch sizes are used for AdamW.
The Optimal Learning Rate
While Liu et al., 2025 suggests their correction factor to the Muon learning rate allows one to reuse the same learning rate used by AdamW, the scaling law obtained here paints a slightly more complex picture.
When using the optimal batch size—which follows a very different scaling law depending on the choice of optimizer—the scaling exponent for the optimal Muon learning rate in terms of model size (N) differs substantially from that of AdamW.
The scaling exponent for the optimal Muon learning rate in terms of dataset size (D) also differs substantially from that of AdamW, most notably having a change in sign. I suspect this occurs because the optimal batch size for Muon grows more slowly asymptotically (B^* propto D^0.4) compared to for AdamW (B^* propto D^0.6), though both scaling exponents should have the same sign when translated into a step law.
Conclusion
In this post, I followed a near-identical training setup as in Part X, changing only the optimizer to be Muon instead of AdamW.
I found Muon has a different scaling law for optimal batch size compared to AdamW.
In addition, I found Muon has a different scaling law for optimal learning rate compared to AdamW, with the scaling exponents for model size N and dataset size D both differing substantially from those of AdamW.