Scaling Laws for Optimal LR and Batch Size - Part VII
Redoing everything with FineWeb, QK-LayerNorm, Independent Weight Decay
Introduction
In Part V we saw how the fitted scaling law for the optimal learning rate was 4x off in its prediction when tested at (N, D) = (4.7B, 100B) parameters and tokens. In Part VI, we saw how Akima spline interpolation improved the forecast when the batch size and/or the learning rate was too coarse.
In this post, I am going to fit hyperparameter scaling laws for Transformer models with QK-LayerNorm and independent weight decay, interventions which will hopefully help to counteract the issues discussed in Part V.1 I will use Akima spline interpolation to predict the optimum beyond the granularity of the sweeps. I’ll again evaluate at test point (N, D) = (4.7B, 100B).
Scaling Laws Setup
Open codebase. I use the research codebase at https://github.com/lucaslingle/babel with branch name ‘sweeps’.
Architecture. I use an architecture similar to Qwen 3, with parametric RMSNorm applied to the residual block inputs and QK-LayerNorm applied to queries and keys with independent scaling parameters for each attention head. I use SwiGLU nonlinearities in the MLP sublayers, with d_ff = 3 * d_model. I use d_head = 128, and n_head = d_model / d_head. I use a locked aspect ratio of d_model/n_layer = 128.
Optimization. I use AdamW with beta1 = 0.9, beta2 = 0.95, eps = 1e^-8. The learning rate schedule uses 2% warmup, followed by cosine decay to a 0.1x factor of the peak.
(N, D) grid. I use model sizes N = 46M, 109M, 368M, 872M and dataset sizes D = 128M, 256M, 512M, 1024M.
(B, \eta) grid. I sweep over batch sizes from 32768 to 2097152 in powers of 2, sweep over learning rates from 0.00012207031 to 0.0078125 in powers of 2^0.5.
Training data. I use the 350B token sample of FineWeb, and the LLaMA-2 tokenizer, which has approximately 32000 vocabulary items including special tokens.
Evaluation. I use 100 held-out batches of size 2097152 tokens for loss evaluation. Evaluation occurs after training has concluded.
Scaling Laws Result
The fitted scaling laws are as follows:
Visualization
Some visualizations of the learning rate scaling law are given below. The scatterplot points correspond to (B, \eta) optima under Akima spline interpolation and the lines correspond to the fitted scaling law. (Click to expand.)
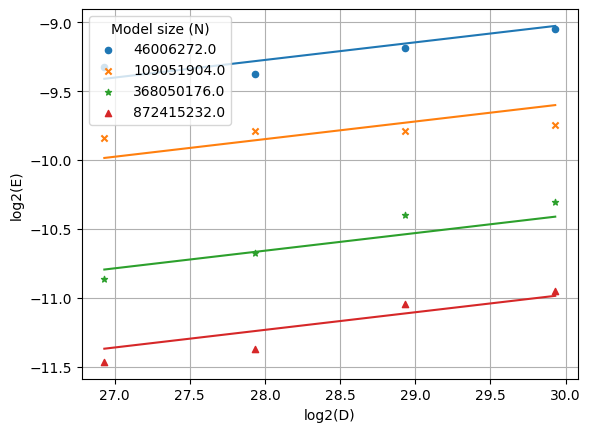
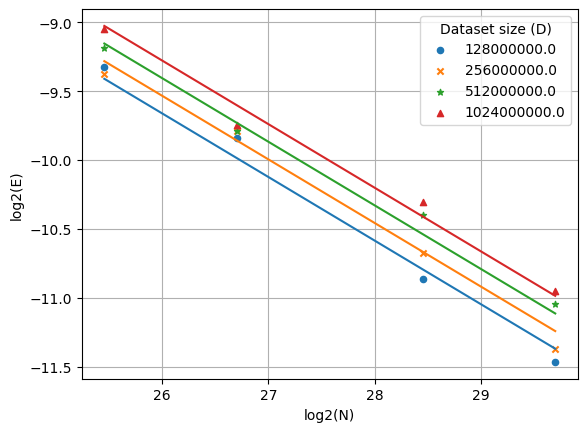
Test Point
The forecasted optimal hyperparameters at test point (N, D) = (4.7 * 10^9, 100 * 10^9) are given by
Verification Setup
I will now verify if the test point’s forecast is approximately correct.
Open codebase. I use the same research codebase https://github.com/lucaslingle/babel with branch name ‘verification’.
Architecture. These details are as above. In particular, QK-LayerNorm is used.
Optimization. These details are as above. In particular, the independent weight decay is set to 1e-5.
(N, D, B) test point. I use N ~ 4.7 billion, D ~ 100 billion, and B = 524,288. The exact architecture uses n_layer = 28, d_model = 3,584. The choice of B comes from evaluating the scaling law for optimal batch size and rounding to the nearest power of two. The exact number of training steps is 200,000.
\eta sweep. The learning rate is swept in powers of two from 2^-13 to 2^-10, inclusive.
Verification Result
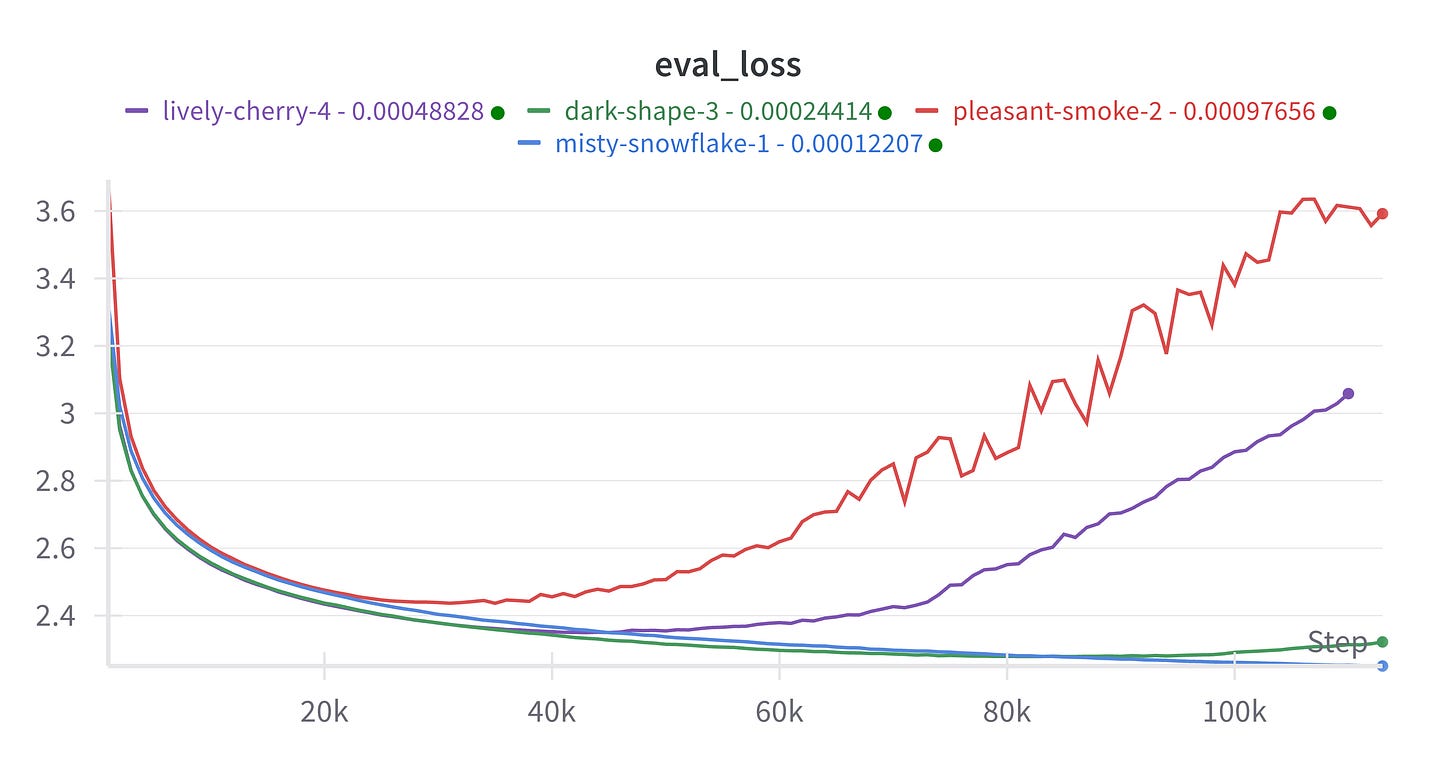
The verification results using QK-LayerNorm and Independent Weight Decay were negative. In particular, for all learning rates in the sweep except 2^-13 ~ 0.0001 we have a phenomenon where the loss curve trends upwards after a while in training:
This indicates that the optimal learning rate \eta^* is ~0.0001 or lower, whereas the scaling law indicated that ~0.0004 was the optimal learning rate.
Conclusion
In this post, I trained 1,456 Transformer models with QK-LayerNorm and Independent Weight Decay. I ran Akima spline interpolation on the loss surface to estimate the optimal batch size and learning rate for each model/dataset size (N, D). Using the estimated optima as regression targets, I performed OLS regression in log-log space to fit scaling laws for the optimal hyperparameters.
I attempted to validate the extrapolation of the scaling laws by training at the scale of (N, D) = (4.7B, 100B). Unfortunately, the forecasted optimal learning rate still did not match the ground truth one at this test point, and the discrepancy is at least as large as before (~4x). I will try to discuss some theoretical causes for this in a later post.
I briefly considered if the beta2 value is too small as discussed in Porian et al., 2024 but I noticed in Figure 16 of that paper that their inferred optima using beta=0.95 still yield a fairly clean scaling law for N > 28 million, and my smallest N was 46 million, so I did not pursue this last direction further.